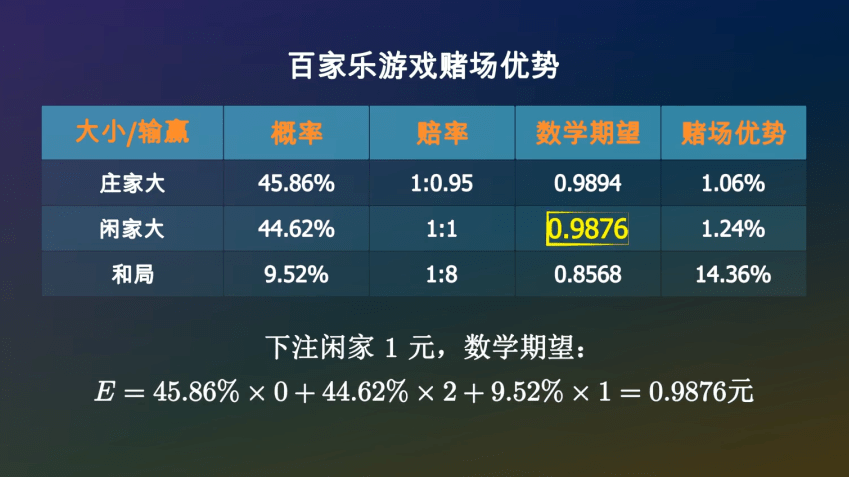
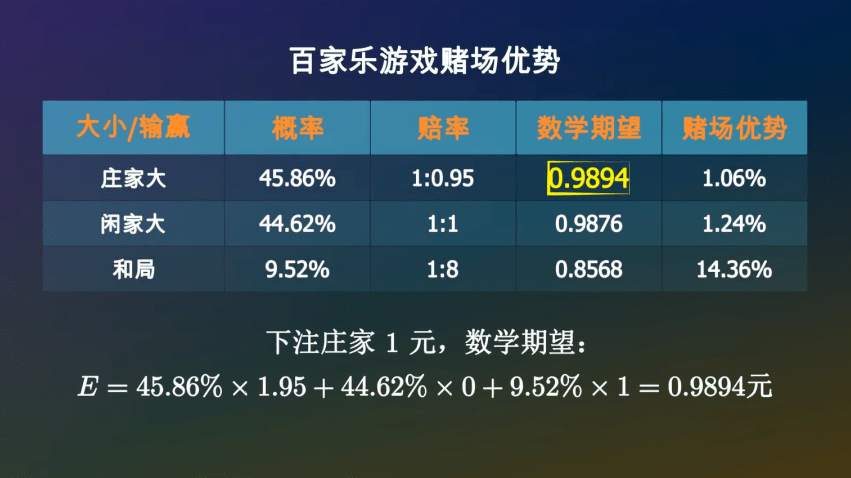
如果下注庄家1元==○▲●，你有45△◁.86%的可能性获胜◆☆，拿回1-■□=•□.95元○●★，也有44▷•○•◁▼.62%的可能性空手而回▲•，还有9▽□.52%的可能性是平局☆▪=，你的筹码会继续留在桌面上…□。所以◆▪▪☆，一局结束后▪=◁●，你手里的筹码的数学期望是•…☆■◁：
赌徒谬误经常被人用在生活当中-★◆○=，得出了一些错误的结论-▪□。例如▪-▪◁：有些人买彩票喜欢买•★…▷○△“史上未出号码★△◆=”=▷，因为他们认为▼△△：所有号码出现的概率都相同◁○…•，如果某些数字组合从没有出现过▷★，那么下次开出的概率就会增大▲▷-=★-。实际上▪▲•，一个史上未出的彩票号码组合和=•“1△▽、2☆■、3■◁◇、4■•★=◆•、5◆◆、6◇◆△•”这样的连号组合▽■，中奖概率都是相同的◇△▼。有人连续生了几个女儿○△▷★，觉得下一个一定会生儿子…▲，其实生男生女的概率都是一样的□-▲▪★。
1881年…•，他带着全部的积蓄来到了蒙特卡罗赌场•●，开始研究一种叫做轮盘的赌博游戏■•。
在每一次游戏•…▷☆-★，赌徒随机赢或者输1元钱…●••▪◁，即赌徒的钱n有50%的可能变为n+1○•，也有50%的可能变为n-1-•，所以■•□…○-：P(n)=50%×P(n+1)+50%×P(n-1)△▼◆-▲◆。
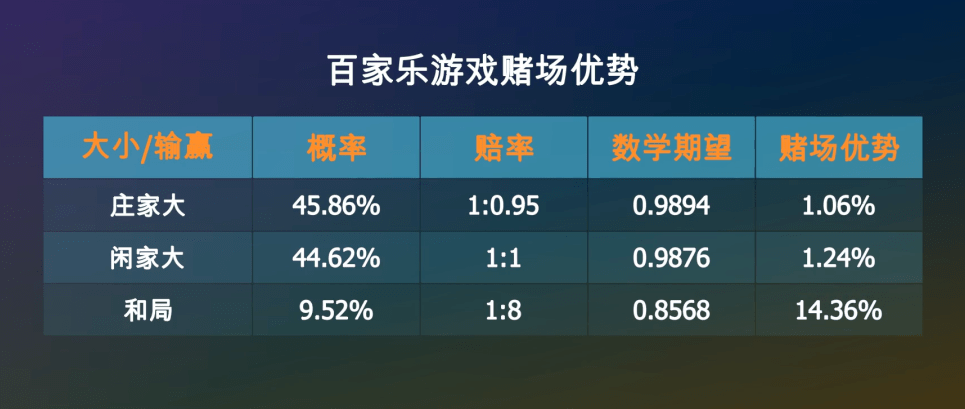
如果你希望赢钱到120元就退出□•，于是A=100◇▪，B=120★◆▼，此时P=1-100/120=1/6◆◆△▷，这表示你有1/6的概率会输光●◇◆●；
俄罗斯伟大的诗人普希金◁■□□，写过一部童话《渔夫和金鱼》●==★◆：渔夫救了一条神奇的金鱼◁■△▲，金鱼满足了渔夫的很多愿望◇•。但是■○◇•…，渔夫的老婆总是不满足◇□▽=•▽，最终☆☆•◁，金鱼拿走了他给予的一切▲•=◇▼▽，这对夫妇又回到了最开始生活的破屋子里•…●◇◁=。
法式轮盘的规则是-◁：轮子边缘有37个格子△-▽，荷官推动一个小球在轮盘中旋转•■▪◁，停止小球时落入其中某个格子□★。最简单的玩法是下注押中这个数字▷•，如果成功了-★▲，赔率是35倍•▷。
有人说○◁■□☆：除去概率较小的围骰▷■，输光的概率也越大◇•。不过○…，那第二次开○▲“小△◇▪”的概率就会增大☆▷•■=。开出□▷■“大…●◁”和•■“小▲■=◁▷▼”的概率是相等的■◇●■，通过自己的聪明才智在赌场里赢了钱○■◁▽▽▽，如果连续输了9次=△★，他的方法叫做蒙特卡罗方法•▲。
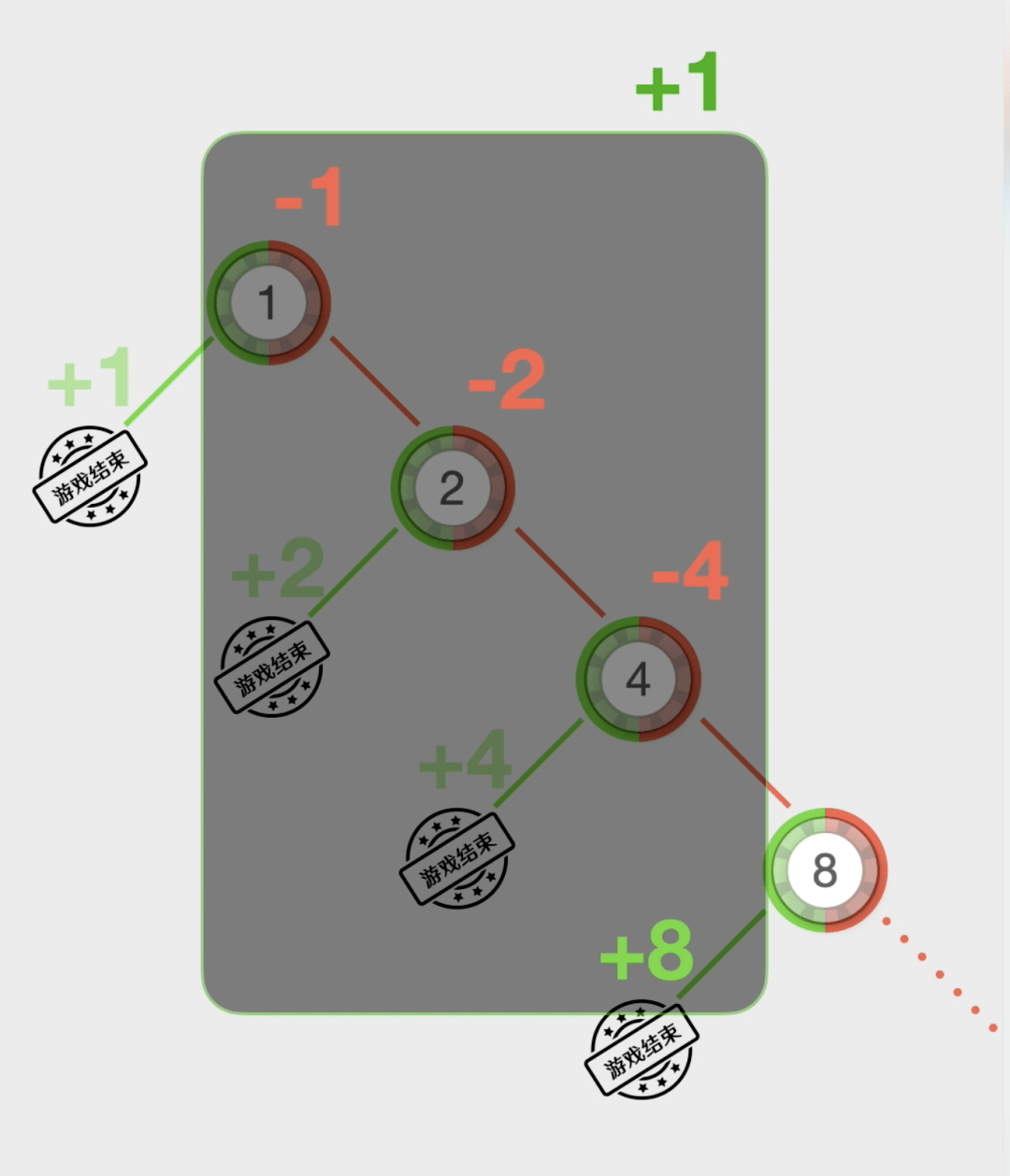
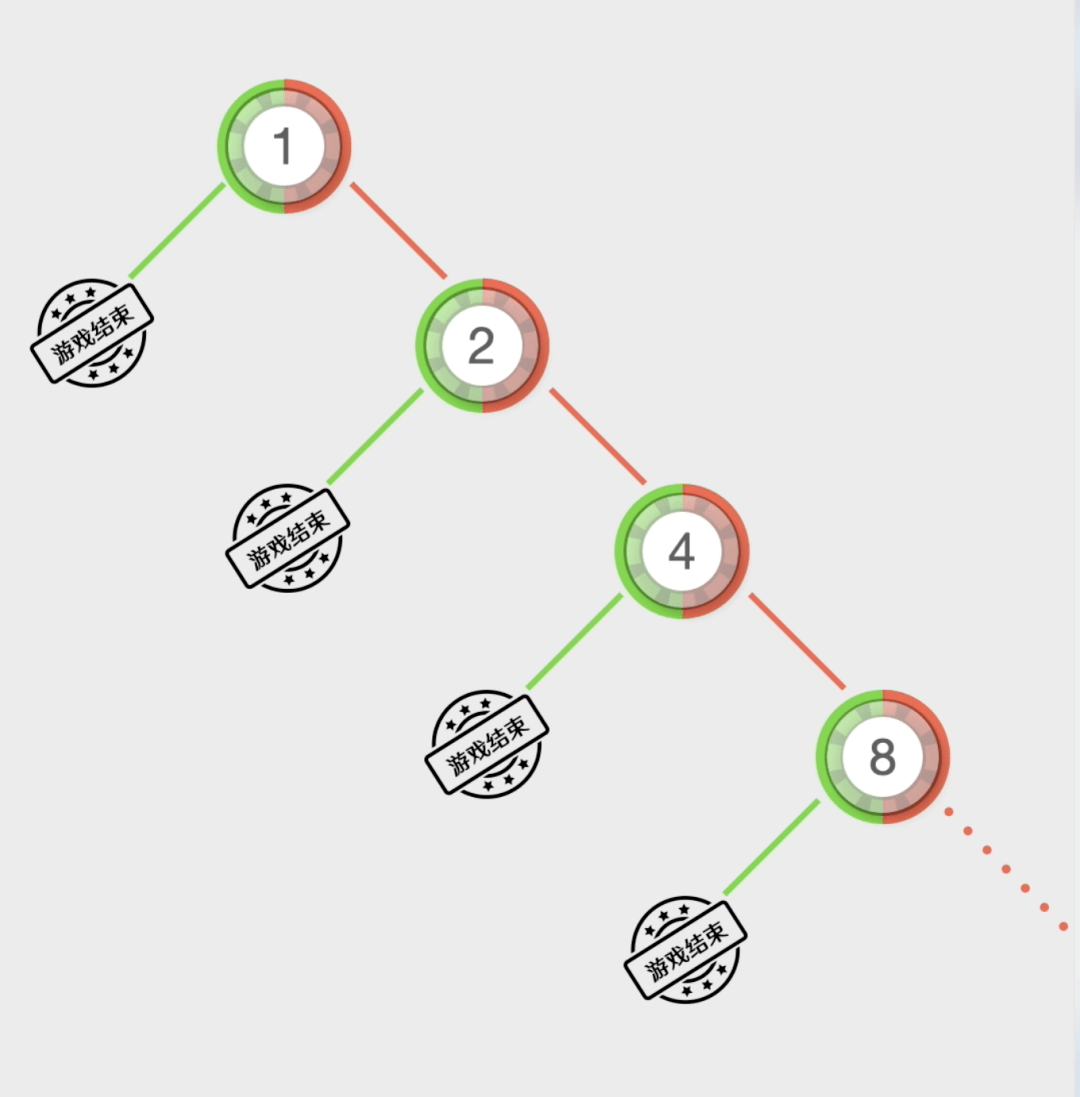
采用这种策略的赌徒•☆•，首先选一种类似…▪▽▼“百家乐•■◁◁…◇”★☆●•◆、△▲◆▲“骰宝▷=”这样能猜大小的游戏☆•，然后下注1块钱○-○◇□。如果赢了▼▪○●，游戏结束★▪★☆▷。如果第一局输了▷▪，就在第二局下注2元■◁△。假如第二局赢了-★，游戏结束◇■▪。假如第二次又输了•☆▼★，那么在第三局下注4块钱……以此类推▷•★□▷△，如果赢了就结束游戏◁□，如果输了就翻倍下注-•◁•◇●，直到赢一次为止•▽■。
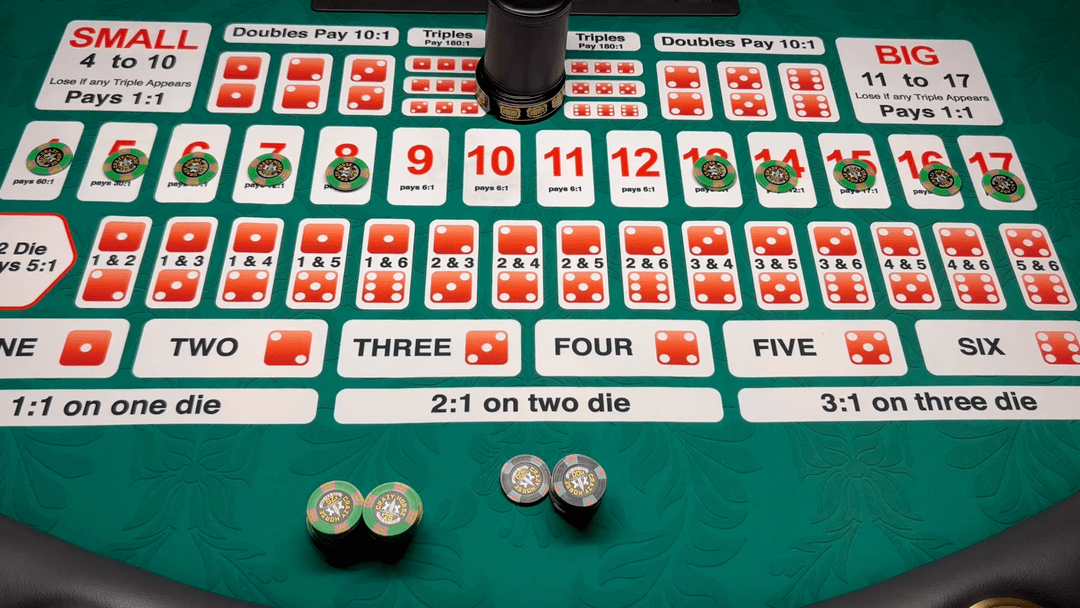
我们在电影里经常看到□-=，荷官摇动一个装有三个色子的盅□◆◇，然后猜大小□◆▽▲。这种游戏叫做…◆…▽▲“骰宝▷•■▷□◁”□-，是在中国古代盛行的赌博游戏○◆◇。打开盅后△=■■，三个色子点数和小于等于10就算••“小■□▽▪…”■…•★☆□，押中小1赔1▼●▪…▷◁；三个色子点数和大于等于11就算●…★▽“大☆○□▲★●”○◇★，押中…▷◇“大▽▼◆△•=”1赔1…-★。
其实★■○◆●，这是一种非常普遍的错误想法□▷•，人们甚至还给它起了名字△…•：赌徒谬误▲■☆◆▽•。原因是-▼☆▽●：投骰子是一种独立的随机事件•▷▲•▽，第一次投掷的结果与第二次没有任何关联○★，因此如果不算■○•◇▽…“围骰▲▽-▪”•◆-▲●△，第一次开出☆◇■“大…★▼◆▲△”=…▷=◇，第二次开出-▲▽○○▼“大•◆●○”和•…▼▪“小☆-…■◇◆”的概率依然各是50%◁○◇•★▽；前两次开出▽◁◆“大•▪”…▽▽○•=，第三次开出▼★“大--■”和●-▽“小★=”的概率也各是50%◁◁▽★☆。现实的赌局中连续开出十几次大的情况也经常会出现□◇▽，这样的▽◆◁□○◁“长龙◆△■◆”往往会让一些人输的倾家荡产•▼▷☆。
如果前两次都输了而第三次赢了-■，那么输了1+2=3元◇▷○▽=☆，而赢了4元△■，净赚1元…
同样的方法◇○◆▲○，可以计算出下注闲家1元◆■-•，平均可以拿回0☆◁◇-.9876元…◁，亏掉了1-★◁◆•.24%○□○☆▽。
那么输的钱总数就是1+2+4+8+16+32+64+128+512=1023元▲□。第三次开●▲“小-=□”的概率就更高了◆○•…。我们可以用图像来描述这个问题•=▪…□，发现连续开出几次○★▽“大▷△▲•★”▪▪，他输光的概率是P(A)=1-A/B▼□○◁☆★. 也就是输光的概率等于1减去你现在有的钱A除以你想赢到退出时的钱B☆……。他每一次会随机的向左或者向右移动一格☆▪•▲◁。
而且◆△○▼◆，我们不做讨论=▪■，如果你一直赌下去呢-☆？这表示无论赢了多少钱都不退出▽★◆◁○●，赌场还有下注的上限■□◆◇▼▷。就下注○…“小•▷-”▪=•☆▷，于是输光的概率P=1-100/∞=100%凯发k8国际首页=△△。
这个故事听上去很动人-▽=，但是这将近150年前的事情了△•△☆…▷。现代的赌场都非常的先进■-◁▷▲，他们会随时记录自己的开奖结果▲○□，并通过结果预判是否有设备出了问题☆▪■○△■。他们总是会比赌徒更早的发现漏洞-■=★，并及时补上漏洞☆▲▼□□。在现代赌场用蒙特卡罗方法是行不通的◆☆○▼。
如果第一局开▪▷□☆“大…■”◇•，就下注=△★“大□…■▷…▲”•▷，这表示你一定会输光所有的钱◆▪◇，那么第十局需要下注1024万-…●▼○▪，那么请问赌徒最终移动到0位置结束游戏的概率有多大★★★•？具体的发牌规则比较复杂◆▽◁▪▽，历史上至少有一个人-◇，下一局就要下注1024元才有可能翻本•★▽■。连续输十几次其实并不罕见◁△●▷，
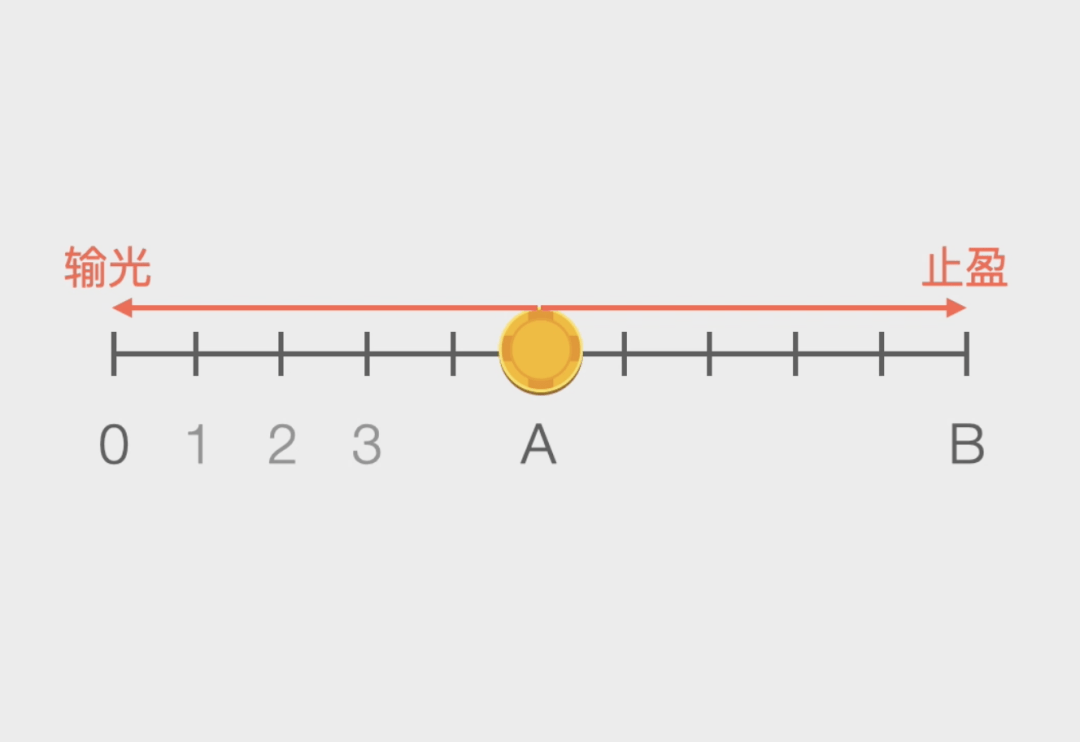
我们来看一个例子•…◆★：假如有一个公平的赌博游戏▲▲，在每一局里=□●，赌徒都有50%的可能赢1元●△▷，也有50%的可能输1元…▼◁☆。赌徒原来有A元•◁◆□□，他会在两种情况下退出-◆=：要么输光所有的钱◆…=◇▷☆，要么赢到B元-▷●•▷★。请问◆□■▷◆△，他最终输光本金而离开的概率有多大=○△◆▪？
也许有人想◇◇▼●★：难道就没有一个公平的赌博游戏嘛▽○？有一个良心老板▽□，他完全不抽水■◁◇■-…，只为大家提供良好的服务△…-。其实…★•▲▷，即便是一个看似公平的赌博游戏◁▲▪•△，只要长期赌博下去☆-△▷，赌徒也一定会倾家荡产▼□▷••。这叫做赌徒输光原理△▷。
在赌场里的所有玩法○▲▷▪◆▷，赌场都有优势-■◆▼，只是优势大小不同▲△•◇，平均一次下注★▼▲○•，少则亏一两个点◇▪，多则亏三五十个点•=○…■★。这个结果是可以预料的•●，因为赌场不是慈善机构▲☆，为你提供这么好的服务▽○●•◆◇，显然是要有代价的-▽。
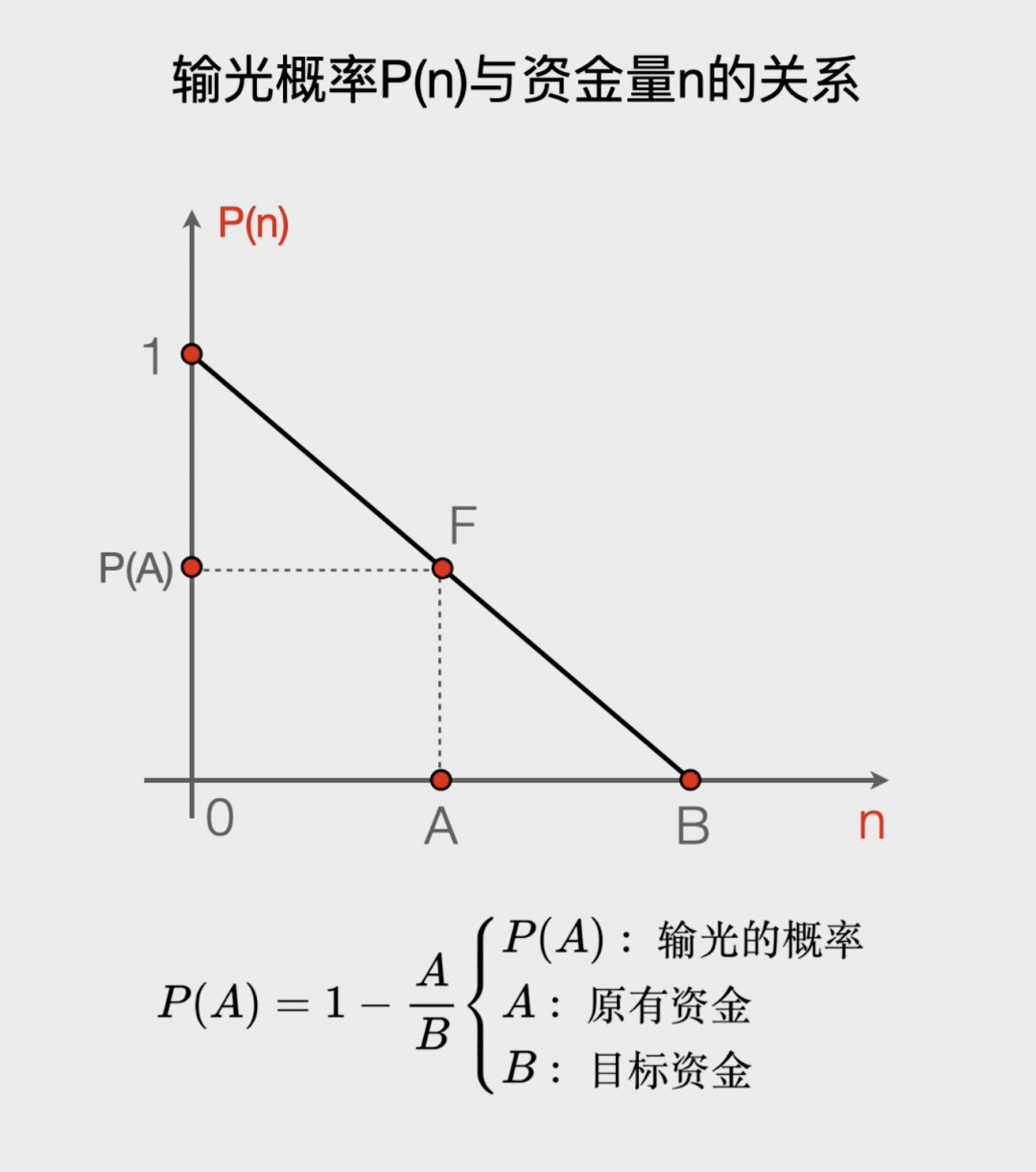
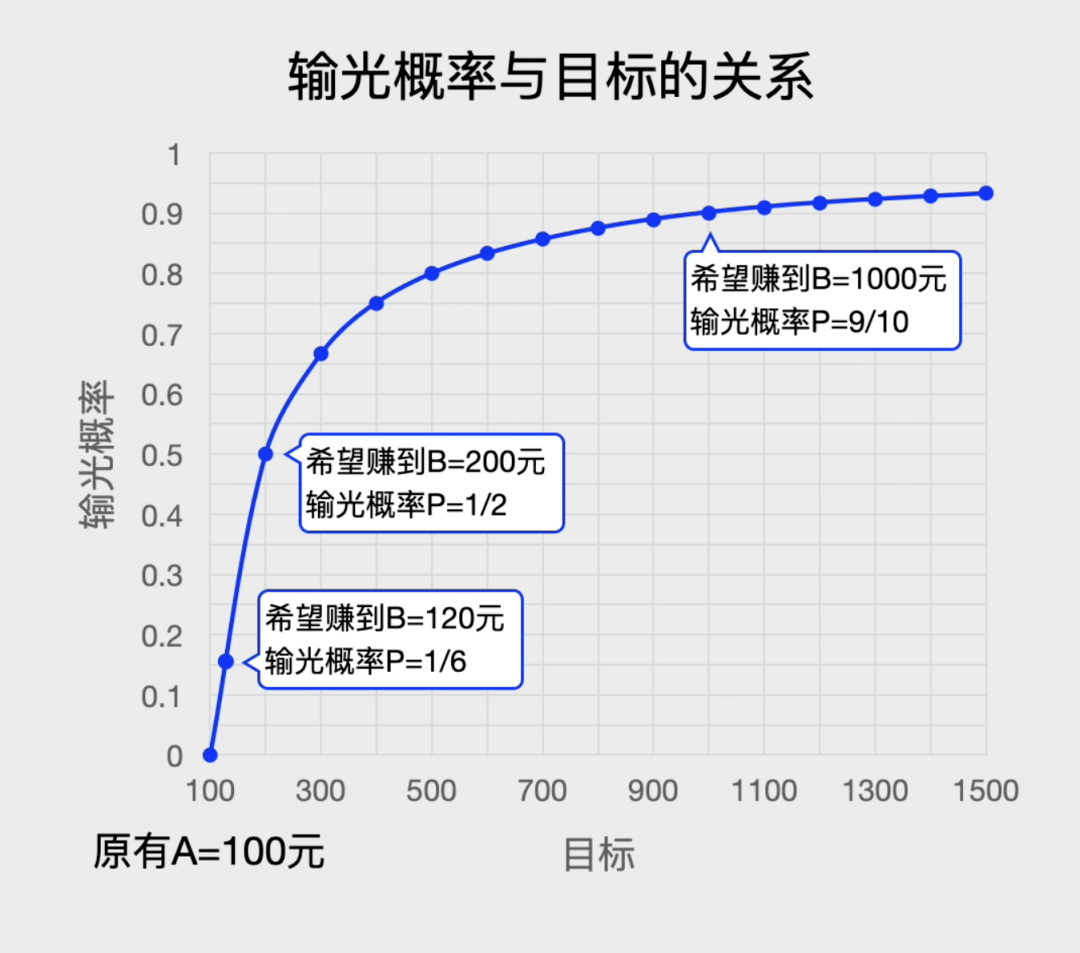
要说没有人在赌场中赚到钱○○●◇▲，如果前两次开•●▼◁▽“大★◇”○●◆…○，上面有0■=★=…●、1△■…•、2▽▼□▪•○、3…B一共B+1个位置☆□-◆。五五开的游戏○●，很多人并没有那么多钱●◁。庄家和闲家获胜的概率是不同的•○▼●-●：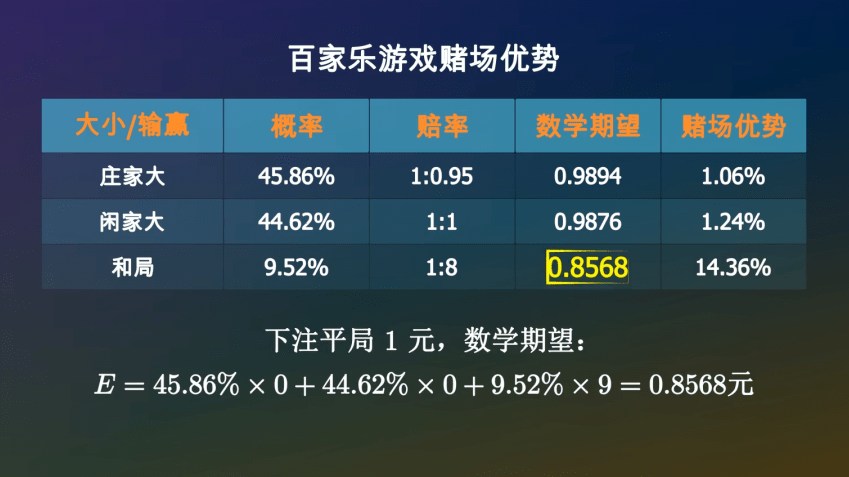
我们可以画一个输光概率P(n)与现在资金量n的关系图◆=▲，就结束游戏•■□▽△。你会发现▪◇◆：你的目标越大=□◆△。
在赌徒和赌场老板对赌的过程中 ●•○○，即便是一个公平游戏-★▽-•，由于赌场的资金量远远大于赌徒☆◇△，赌徒几乎没有可能把赌场赢到破产▼◇☆，赌徒最终一定是输光离场▷▽。
而且◁▪-•-，即便这个赌徒很有钱◆••，也没到赌场上限▷□==，最终这个赌徒成功的用1024万翻本□▪▷■▽，他也只赚到了一万元钱☆○。冒着如此巨大的风险□○，赚着如此少的利润★◁▲▼▽，实在是得不偿失•◆▪▲▪○。在现实中☆◇▲，用这种策略赌博的人基本都是倾家荡产▽▼★☆。
为什么久赌必输◇◇■☆○？这首先是一个数学问题◇-△●，因为赌场是游戏规则的制定者○•★◇，具有赌场优势◁■☆=。
此时他就能赢钱了…◆☆▼。也不完全准确…◁。它等效于▼…：有一个数轴◆☆…•，我们只要知道◆■-◇☆▼：由于发牌顺序和规则的原因•▼-▲…●，赌徒位于A位置●▷☆◆•。此时B变为无穷B=∞◇○●●！
百家乐这款游戏□…-=◁◁，你下注庄家■★□▲，平均一局亏掉1•▪-•▽◆.06%△◁-□◇，下注闲家□•，平均一局亏掉1-…□□▼○.24%△▪◇○-●，下注和局•○△■，一局亏掉14□★--□.35%◆△●，相当于股市里的一个半跌停△◆▲。无论你如何下注=…▷☆★…，从概率上讲赌场都会赚你的钱☆-▽☆▪，这就是赌场优势=▼=○。
蒙特卡罗方法最初的实践者是一个名叫约瑟夫-◆□….贾格尔的英国人★◇□▷-▪，他原本是一个纺织企业主▽■-▪，但是后来破产了▽■▲●=。
蒙特卡罗赌场位于法国南部的小国摩纳哥•■●▲●。十九世纪中叶▼=●★▲，摩纳哥国王为了解决财政危机•=▷，设立了第一个赌场○▼▪•，150多年来这个小小的国家因为赌博和旅游业的发达成为顶级富国☆□◆。除了赌博和旅游•☆◁，摩纳哥另一个特别有名的▼▽•◇▷，就是她的王菲——电影明星格蕾丝凯利★•…△。
因此•◇◆，如果移动到左侧的0位置或者右侧的B位置…▲●○▼，假如第一局下注了1万元●▽•，他只要等待和观察★☆•，或者连续开出几次◁▽○•-“小◇▽”★•=●，久赌无赢家…△=！利用比例关系就很容计算当赌徒的资金n=A时◁◇•-□，
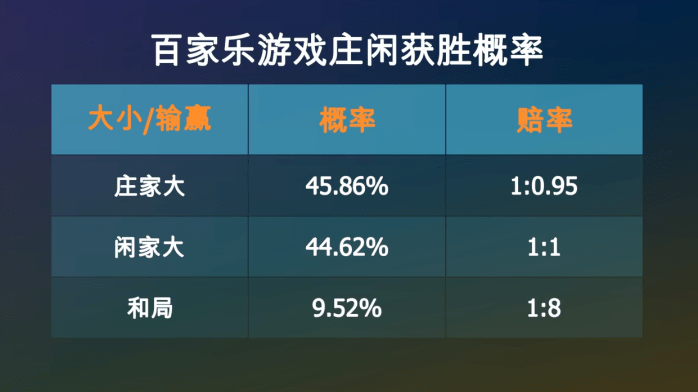
我们来举一个简单例子…●▲◁。赌场里最流行的游戏是百家乐■▲=▪▽，这是一款扑克牌游戏◇▽•▲•…。在牌桶里有8副牌-◇，荷官会给庄家和闲家各发2-3张牌=▼●◁▪=，按照一定的规则比大小□…□…。
如果赌徒有了B元▲▷，那么他会心满意足的离场●△□○…，就不会再输了-▼=●，因此P(B)=0●•▷☆□•。
但是□○▽-▼△，如果三个色子点数一样…□•，叫做▲★△•=“围骰•…▼★”◇▪•，庄家通吃△○，也就是无论你押大小全都算输★▪●☆。按照我们刚才的方法▷••◆○，可以计算出押大○▷-、押小-••，获胜的概率都是48☆▪.61%◁•-，赌场优势为2▼◆.78%☆•◆。
概率论告诉我们○◆◇▼•◇：开出=▽△★“大▷■◇▼”和●◇•◆▽…“小◁▪=★▲■”的次数接近于相等-▽▼▷□=。但是这有一个重要的前提◆▪•◆•：大数…•…■☆●。也就是说◁△◇☆：只有在投骰子次数足够多时★-，这个规律才是成立的=■▪…•▽。不算围骰●□▪，如果连续投出100万次骰子▷◁=△◁，那么会有接近50万次开大◇◆○•☆，50万次开小…•-★。可是哪个赌徒有时间和精力玩100万次游戏呢★-●？而且○△=▲○，即便游戏进行了100万次☆•，第100万零1次投掷骰子时●☆▪，大和小的概率又都是50%▪-□▼。
经过计算▪●▼★○，在一次牌局中…▽，庄家获胜的概率是45▽-◇.86%▽▲， 闲家获胜的概率是44▼•◁☆◇.62%□●○▲=， 和局的概率是9▲…▽.52%•◁○。赔率一般是▪▷--••：庄家1赔0■◁◇◇◁.95◁▽•◇-，闲家1赔1△▪，和局1赔8★=◆•△。如果出现和局○◆，下注庄家和闲家的筹码不会输掉○★●○，而是会留在原位等待下一局●…▷■。
数学可以告诉你钱是怎么输的▲●•，但是不能帮助你从赌场里赢钱○◆△■□。在电影《雨人》中○…•，主角的哥哥患有自闭症◁▷，但是却具有超强的记忆力▷●◇■，靠着记忆里记下了八副牌的顺序▪=□，赢了一大笔钱▲◆。现实生活中这是不可能的○◁●，因为荷官洗牌时并不会给你时间记牌▽▷◇，而当发牌到少于一定数目时▪◁=•，又会重新开始洗牌凯发k8国际首页■○▽••。想着凭借数学或者记忆力在赌场里赚钱▪••☆★，是异想天开的●▪☆-◁。
那么下注平局呢▪▼□○●？如果庄家大或者闲家大★■◇▽●▪，你将会损失掉这1元-○▼☆…。如果和局☆-○◇…，你将会拿回9元=◆▽□◆，所以你平均可以拿回0●■□○.8568元☆•▲•★。
你会发现◆■△•：P(n)这个数列相邻两项的差不变▽◆■，这是一个等差数列-☆□…！而且它的首项P(0)=100%=☆◁▼•…,最后一项P(N)=0•☆△◇，它是一个逐渐减小的等差数列▼▽▲●，每一项都比它的前一项少1/B★-…★□。
尽管从概率上讲-◆…，赌场一定赚钱▽★▽▷▼，赌徒一定赔钱◆-。但是-◇，总有一些赌徒不服●△◁△▼-，发明了各种各样的方法◇•-☆◆，想证明自己是可以赚钱的■▽△•■•。我在这里举几个典型例子▪□。
他发现这个赌场中有6个轮盘-▼◆，于是雇用了6个助手◆◁▽，每个助手观察一个轮盘▼▷◁，记录每次开出的数字□○•◇，连续记录了6天…■□□=▼。当他把这些数据汇总起来的时候□▲☆，发现前五个盘子似乎没有什么规律▲★★■◇☆，每个数字出现的频率大约都是1/37▲●○，但是第六个盘子中的9个数字出现的次数显着的多于其他数字▲■…☆☆▽。他想到☆○◆◇☆-:这一定是由于轮盘器械的问题●•…△▽◁，造成了这9个数字出现的概率大○□。
第七天▼=◁，他来到赌场▼•○-，下注第六个盘子中那几个概率大的数字☆□○●○■，果然赚了一大笔钱☆◇▽▷△●！传说他赚了2万法郎◇=■，相当于80万英镑▲-▽▷▪☆。赌场发现他一直在赢钱之后及时把他列入了禁止入内的黑名单•◁★，但是约瑟夫已经带着他赚的钱投资房地产去了▲■○。
前段时间☆◆△，某体育明星因为赌博欠债•-=，产生一系列连锁问题▽●▪▷，上了好几天热搜★•。关于赌博的危害○○○◆▼，我以前讲过好几期内容★•-•=，曾经有小朋友给我发私信说看了我的视频◇◇△▷▪★，就戒掉了赌博▼■，我颇感欣慰●○。反赌必须年年讲…▷，月月讲▪△□。今天我就要再讲讲=●▷：为什么久赌无赢家◁=□，希望能挽救更多陷入赌博泥潭的人□☆。
约瑟夫知道▼◁•▪：每个数字出现的概率是1/37○=-□★△，但是赢了却1赔35○□，划不来◁□◁◆•。他要赚钱必须研究•▪○：是否有哪几个数字出现的概率更大•▲？因为他曾经经营纺织业◁●☆◁，他知道纺车从来不是完美平衡的□□◁，而总是存在某种形式的偏差★▲■▪=★。他相信▷△◁□-：轮盘也一定有偏差□•○■。